施工企业八大员郑州网站seo优化
28.找出字符串中第一个匹配项的下标
目录
- 28.找出字符串中第一个匹配项的下标
- 题目描述
- 解法一:朴素的模式匹配
- 解法二:KMP算法
- KMP解决的问题类型
- 最长公共前后缀
- KMP算法过程
- next数组的构建
- 代码实现
题目描述
给你两个字符串haystack和needle,请你在haystack字符串中找出needle字符串的第一个匹配项的下标(下标从0开始)。
如果needle不是haystack的一部分,则返回-1。

解法一:朴素的模式匹配
第一种容易想到的方法就是暴力求解法,也叫做朴素的模式匹配:
简单的来说就是,从主串hyastack和子串needle的第一个字符开始,将两字符串的字符一一对比,如果出现某个字符不匹配,主串haystack回溯到第二个字符,子串needle回溯到第一个字符再进行一一对比,如果再次出现某个字符不匹配,则主串回溯到第三个字符,子串回溯到第一个字符…以此类推,直到子串t的字符全部匹配成功。
这道题目最为直观的解法是:依次枚举haystack中的每个字符作为[发起点],每次从原串(haystack)的[发起点]和匹配串(needle)的[首位]开始尝试匹配
- 匹配成功:返回本次匹配的原串的[发起点]
- 匹配失败:枚举原串的下一个[发起点],重新尝试匹配
public int strStr(String haystack, String needle) {int n = haystack.length();int m = needle.length();for(int i=0;i+m<=n;i++){boolean flag = true;for(int j=0;j<m;j++){if(haystack.charAt(i+j)!=needle.charAt(j)){flag = false;break;}}if(flag){return i;}}return -1;}
解法二:KMP算法
当出现经典的字符串匹配时,我们选择使用KMP算法。
KMP解决的问题类型
kmp算法的作用是在一个已知字符串中查找子串的位置,也叫做串的模式匹配。
比如主串s=“university”,子串t=“sit”。现在我们要找到子串t在主串s中的位置,这点相信大家很容易就看出来了,是在第七个位置。
当然,在字符串非常少的时候,“肉眼观察法”不失为一个好方法,但如果要你在一千行一万行文本中找一个单词,我觉得一般人都找不到。
第一种容易想到的方法就是刚刚的解法一,暴力求解法,也叫做朴素的模式匹配:
简单的来说就是,从主串s和子串t的第一个字符开始,将两字符串的字符一一对比,如果出现某个字符不匹配,主串s回溯到第二个字符,子串t回溯到第一个字符再进行一一对比,如果再次出现某个字符不匹配,则主串s回溯到第三个字符,子串s回溯到第一个字符…以此类推,直到子串t的字符全部匹配成功。
但是这个方法真的很慢,因为求一个子串的位置需要太多步骤,而且很多步骤根本没必要。
这种暴力解法在最好的情况下算法的时间复杂度为O(n),即子串的n个字符正好等于主串的前n个字符,而最坏的情况下时间复杂度为O(n*m)。但是好在这种算法的空间复杂度为O(1),即不消耗空间而消耗时间。
下面进入正题,KMP算法是如何优化这些步骤的。
其实KMP算法的主要思想就是,牺牲空间换时间。
我们回头看一遍解法一的暴力方式,为什么这么慢呢?是因为我们回溯的步骤太多了,所以我们应该减少回溯的次数。
怎样做呢?比如上面第一个图:当字符’d’与’g’不匹配,我们保持主串的指向不变
主串依然指向’d’,而把子串进行回溯,让’d’与子串中’g’之前的字符再进行比对。
如果字符匹配,则主串和子串字符同时右移。
至于子串回溯到哪个字符,这个问题我们先放一放。
最长公共前后缀
这里提出一个概念:字符串的最长相等前缀和后缀
举个例子
字符串abcdab
前缀的集合:{a,ab,abc,abcd,abcda}
后缀的集合:{b,ab,dab,cdab,bcdab}
此时最长的公共前后缀就是ab
OK,现在我们已经会求一个字符串的前缀,后缀,以及公共前后缀了,这个概念很重要。
之前留了一个问题,子串回溯到哪个字符,现在可以着手解决了
KMP算法过程
现在我们看一个图:第一个长条代表主串,第二个长条代表子串,红色部分代表两串中已匹配的部分
绿色和蓝色部分分别代表主串和子串中不匹配的字符

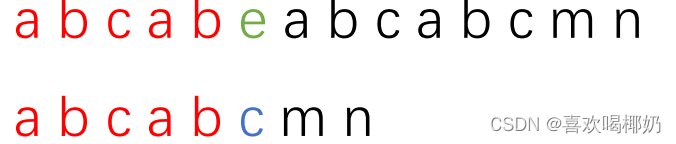
现在发现了不匹配的地方,我们根据KMP算法的思想,保持主串位置不动,将子串向后移,现在我们要解决的,就是移动多少的问题
之前提到的最长公共前后缀的概念有用处了。
因为红色部分,即已经匹配的部分也会有最长相等前后缀,如下图

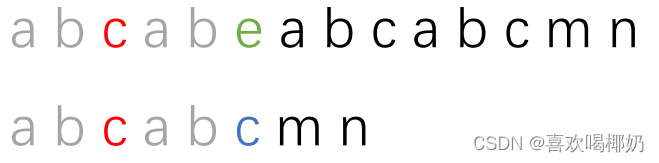
我们发现,之前“abcab”红色部分的最长公共前后缀为“ab”,所以,我们把前缀“ab”和后缀“ab”都标成灰色
子串移动的结果就是让子串的红色部分最长相等前缀和主串红色部分最长相等后缀对齐

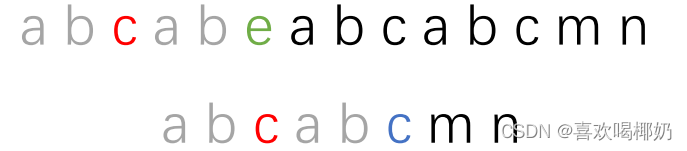
这一步弄懂了,KMP算法的精髓我们就掌握了,接下来的流程就是一个简单的循环过程。
事实上,每一个字符前的字符串都有最长相等前后缀,而且最长相等前后缀的长度是我们移位的关键,所以我们单独使用一个next数组存储子串的最长相等前后缀的长度,而且next数组的数值只与子串本身有关。
所以,next[i]=j的含义是:下标为i的字符前的字符串最长相等前后缀的长度为j。
我们可以算出上图中子串“abcabcmn”的next数组为next[0]=-1(前面没有字符串单独处理)
| 字符 | a | b | c | a | b | c | m | n |
|---|---|---|---|---|---|---|---|---|
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| next[i] | -1 | 0 | 0 | 0 | 1 | 2 | 3 | 0 |
再看一眼刚刚是哪里出现了不匹配
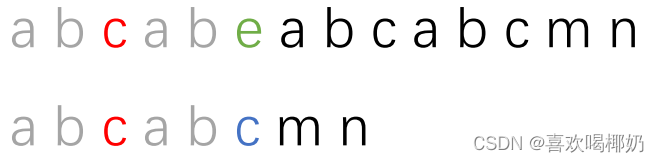
即s[5]!=t[5]
我们把子串移动,也就是让s[5]与t[5]前面字符串的最长相等前缀的后一个字符再比较,而next[5] = 2,所以我们让子串t的第三个字符和刚刚主串的位置对齐开始比较
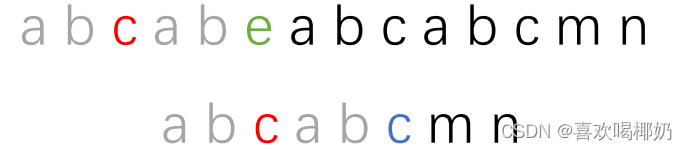
以此类推,直到将子串匹配完为止
这里我们可以总结一下,next数组的作用:
- 1、next[i]的值表示下标为i的字符前的字符串的最长相等先后缀的长度
- 2、表示该处字符不匹配时应该回溯到的字符的下标
next数组的构建
接下来,我们来看看next数组是如何被预设出来的。
假设有匹配串aaabbab,对应的next数组构建过程如下
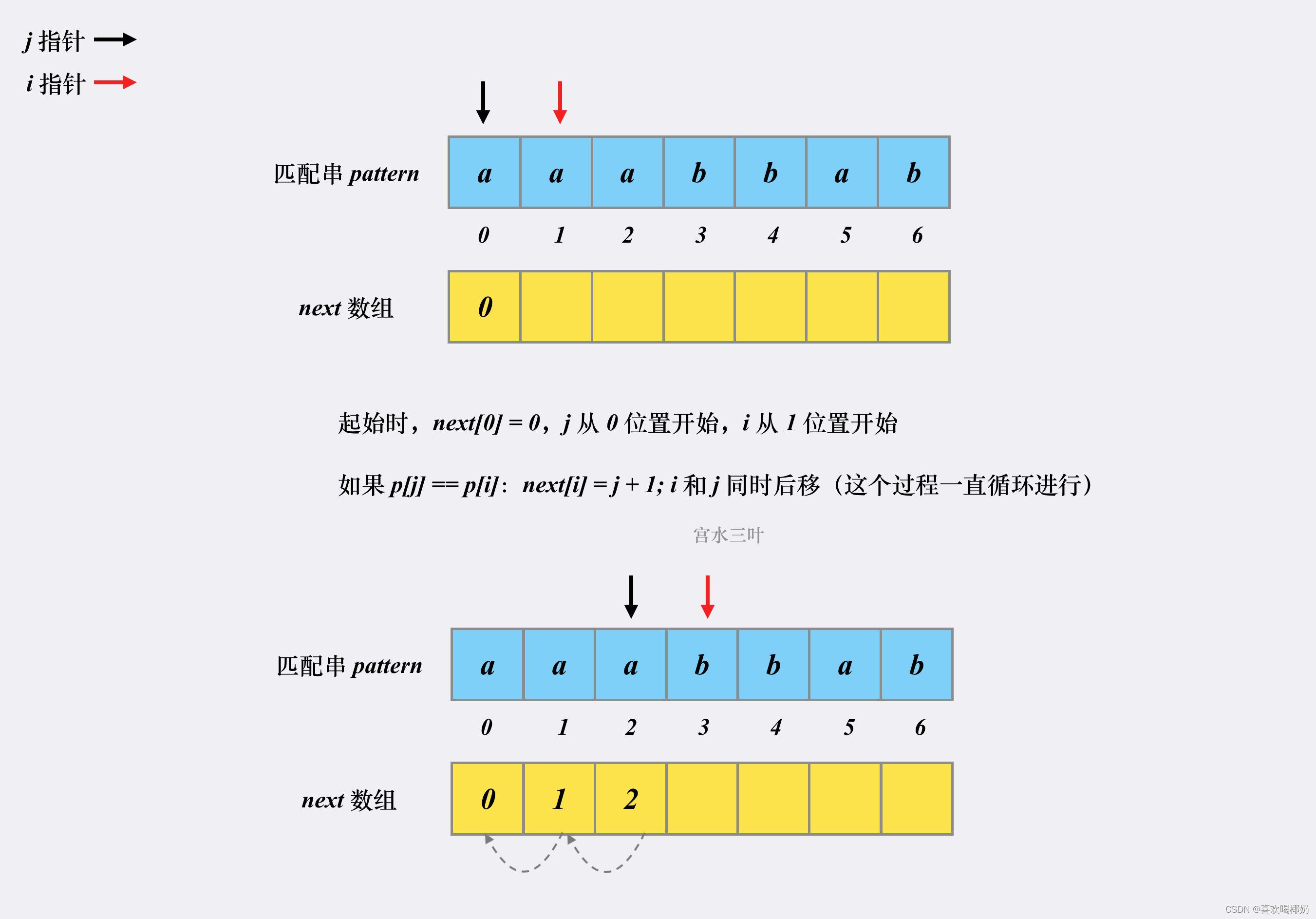
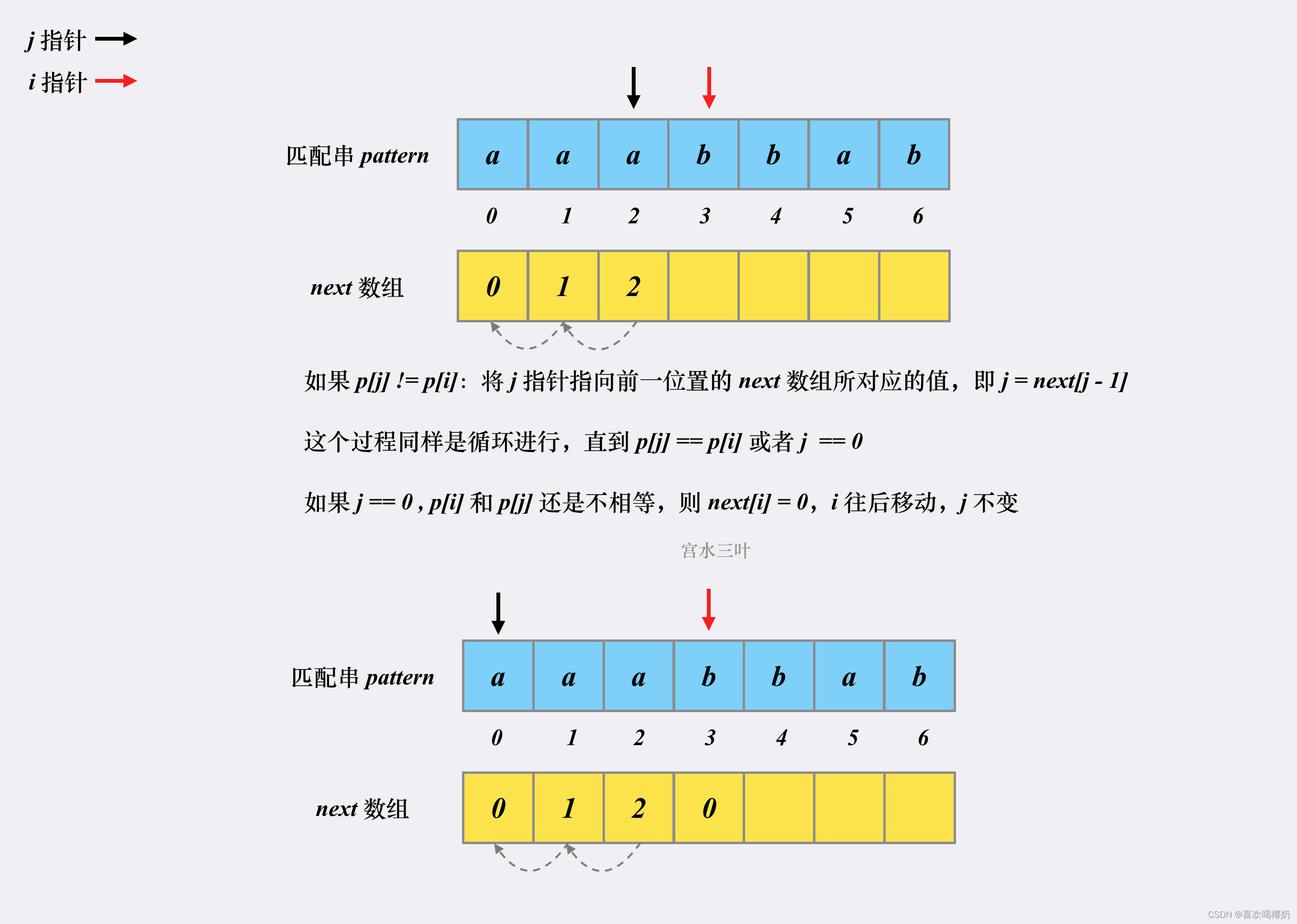
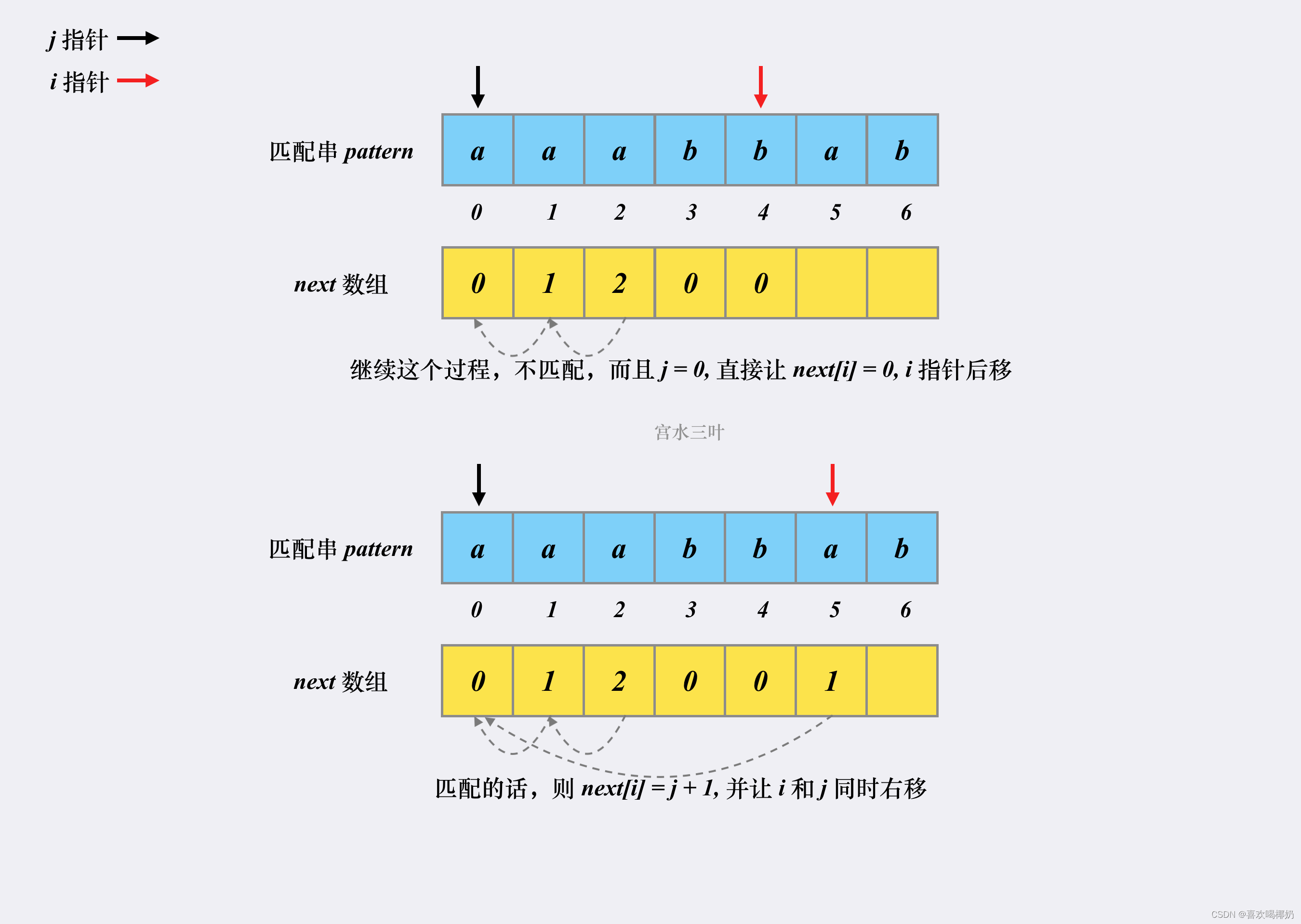
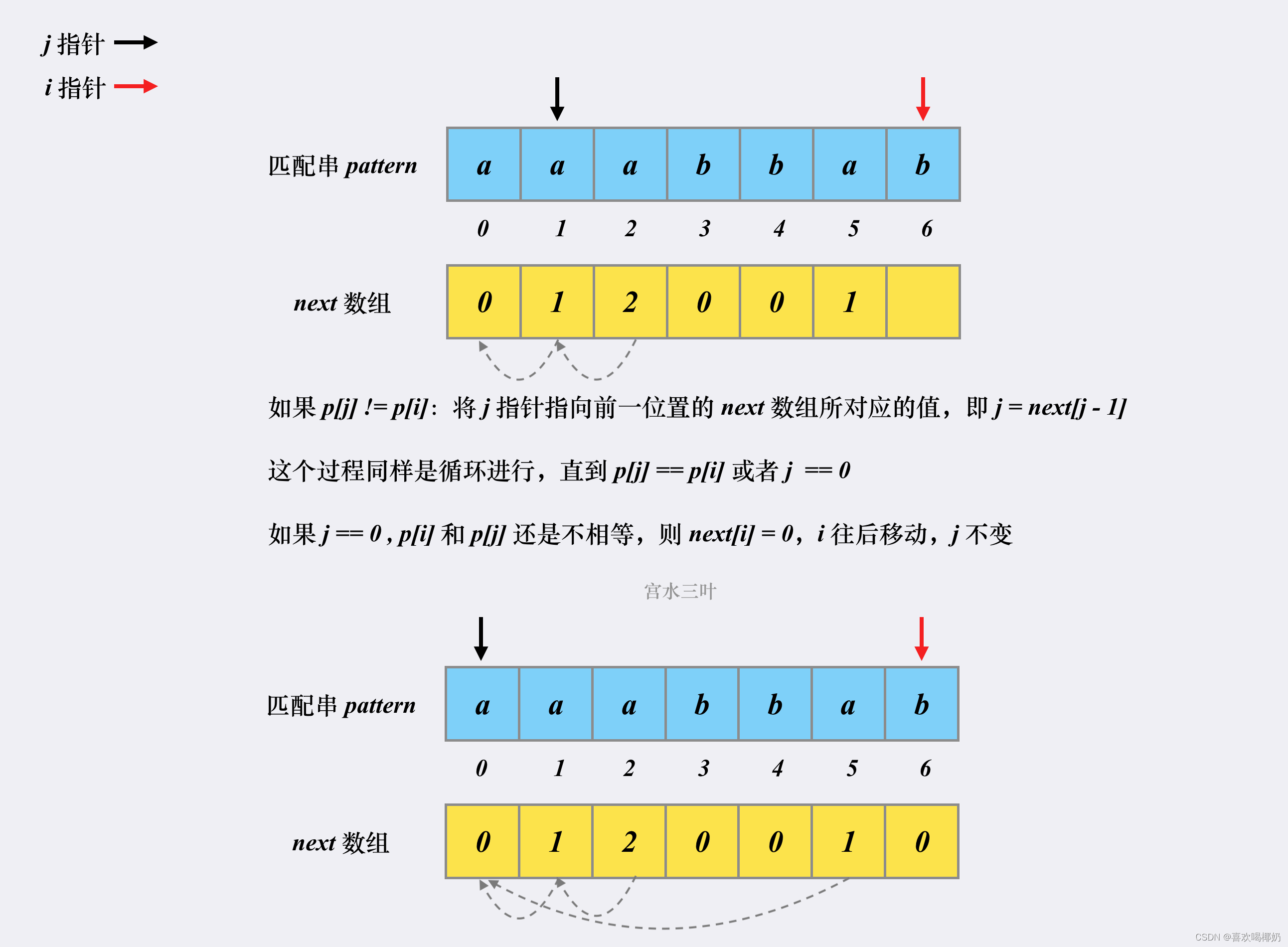
代码实现
public int strStr(String haystack, String needle) {if(needle.isEmpty()){return 0;}//分别读取原串和匹配串的长度int n = haystack.length(),m = needle.length();//原串和匹配串前面都加空格,使其下标从1开始haystack = " "+haystack;needle = " "+needle;//转成字符数组char[] s = haystack.toCharArray();char[] p = needle.toCharArray();//构建next数组,数组长度为匹配串的长度(这是因为next数组是和匹配串相关的)int[] next =new int[m+1];//构造过程,i=2,j=0开始,i小于等于匹配串的长度for(int i=2,j=0;i<=m;i++){//匹配不成功的话,j=next[j]while(j>0&&p[i]!=p[j+1]){j = next[j];}//匹配成功的话,先让j++if(p[i]==p[j+1]){j++;}//更新next[i],结束本次循环,i++next[i] = j;}//匹配过程,i=1,j=0开始,i小于等于原串长度for(int i=1,j=0;i<=n;i++){//匹配不成功 j=next(j)while(j>0&&s[i]!=p[j+1]){j=next[j];}//匹配成功的话,先让j++,结束本次循环后i++if(s[i]==p[j+1]){j++;}//整一段匹配成功,直接返回下标if(j==m){return i-m;}}return -1;}
