当前位置：首页 > news >正文

宣传类的网站怎么做/广告软文代理平台

news 2025/7/31 21:33:21

宣传类的网站怎么做,广告软文代理平台,网站建设ppt方案,建设政府网站来源0x3f：https://space.bilibili.com/206214 回溯分为【子集型回溯】【组合型回溯】【排列型回溯】文章目录回溯基本概念[17. 电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)子集型回溯（分割问题也可以看…

来源0x3f：https://space.bilibili.com/206214

回溯分为【子集型回溯】【组合型回溯】【排列型回溯】

文章目录

回溯基本概念
- [17. 电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)
子集型回溯（分割问题也可以看作枚举分割点==>子集型）
- [78. 子集](https://leetcode.cn/problems/subsets/)
- - 方法一：输入的视角（每个节点可以选择选和不选）
  - 方法二：答案的角度（枚举第一个数选谁、第二个数选谁）
- [131. 分割回文串](https://leetcode.cn/problems/palindrome-partitioning/)
- - 思路：设每两个相邻字符间有逗号，枚举每个逗号结束位置。这样就变成了[78. 子集]问题
- [784. 字母大小写全排列](https://leetcode.cn/problems/letter-case-permutation/)
- [93. 复原 IP 地址](https://leetcode.cn/problems/restore-ip-addresses/)
组合型回溯（剪枝技巧）
- [77. 组合](https://leetcode.cn/problems/combinations/)
- [216. 组合总和 III](https://leetcode.cn/problems/combination-sum-iii/)
- [22. 括号生成](https://leetcode.cn/problems/generate-parentheses/)
排列型回溯（棋盘问题也是排列型回溯）
- [46. 全排列](https://leetcode.cn/problems/permutations/)
- [51. N 皇后](https://leetcode.cn/problems/n-queens/)

回溯基本概念

回溯三问：

1、当前操作？

2、子问题？

3、下一个子问题？

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

17. 电话号码的字母组合

难度中等2314

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。

回溯三问：

1、当前操作？ 枚举 path[i] 要填入的字母

2、子问题？ 构造字符串>=i 的部分

3、下一个子问题？ 构造字符串>= i+1 的部分

class Solution {private static final String[] arr = new String[]{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};List<String> res = new ArrayList<>();public List<String> letterCombinations(String digits) {if(digits.equals("")) return res;dfs(digits, 0, new StringBuilder());return res;}public void dfs(String digits, int i, StringBuilder sb){if(i == digits.length()){res.add(sb.toString());return;}String str = arr[digits.charAt(i) - '0'];for(int j = 0; j < str.length(); j++){sb.append(str.charAt(j));dfs(digits, i+1, sb);sb.deleteCharAt(sb.length()-1);}}
}

子集型回溯（分割问题也可以看作枚举分割点==>子集型）

子集型回溯：每个元素都可以选和不选

回溯三问：

**1、当前操作？**枚举第 i 个数选/不选

2、子问题？ 从下标 >=i 的数字中构造子集

3、下一个子问题？ 从下标 >=i+1 的数字中构造子集

78. 子集

难度中等1931

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

题解：

方法一：输入的视角（每个节点可以选择选和不选）

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> cur;public List<List<Integer>> subsets(int[] nums) {cur = new ArrayList<>();dfs(nums, 0);return res;}// 每个节点可以选择选和不选public void dfs(int[] nums, int i){if(i == nums.length){res.add(new ArrayList<>(cur));return;}dfs(nums, i+1);cur.add(nums[i]);dfs(nums, i+1);cur.remove(cur.size()-1);}
}

方法二：答案的角度（枚举第一个数选谁、第二个数选谁）

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> cur;public List<List<Integer>> subsets(int[] nums) {cur = new ArrayList<>();dfs(nums, 0);return res;}// 每个节点可以选择选和不选public void dfs(int[] nums, int i){// 关键在这里， 递归入口每次记录答案res.add(new ArrayList<>(cur));if(i == nums.length){return;}for(int j = i; j < nums.length; j++){cur.add(nums[j]);dfs(nums, j+1);cur.remove(cur.size()-1);}}
}

131. 分割回文串

难度中等1387

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

输入：s = "a"
输出：[["a"]]

提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

思路：设每两个相邻字符间有逗号，枚举每个逗号结束位置。这样就变成了[78. 子集]问题

方法二：答案的角度（枚举字串结束位置）

class Solution {List<List<String>> res = new ArrayList<>();List<String> cur;public List<List<String>> partition(String s) {cur = new ArrayList<>();dfs(s, 0);return res;}public void dfs(String s, int i){if(i == s.length()){res.add(new ArrayList<>(cur));return;}//枚举字串结束位置(设以j结尾是否符合要求)for(int j = i; j < s.length(); j++){//判断一下[i, j] 部分是否为回文串String str = s.substring(i, j+1);if(isrev(str)){cur.add(str);dfs(s, j+1);cur.remove(cur.size()-1);}}}public boolean isrev(String str){int left = 0, right = str.length()-1;while(left < right){if(str.charAt(left) != str.charAt(right))return false;left++; right--;}return true;}
}

784. 字母大小写全排列

难度中等515

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4"
输出: ["3z4","3Z4"]

提示:

1 <= s.length <= 12
s 由小写英文字母、大写英文字母和数字组成

题解：

DFS 回溯看到题目要求组合或者集合，马上想到可以用回溯法：

回溯法本来是说对于每个元素都先考虑放它的情况，再考虑不放它的情况；

放在这道题的背景里就是，对于每个字母，先考虑放它，再考虑放它的另一种大小写形式。

class Solution {List<String> res = new ArrayList<>();public List<String> letterCasePermutation(String s) {dfs(s, 0, new StringBuilder());return res;}public void dfs(String s, int i, StringBuilder sb){if(i == s.length()){res.add(new String(sb.toString()));return;}// 不改sb.append(s.charAt(i));dfs(s, i+1, sb);sb.deleteCharAt(sb.length()-1);//改if(s.charAt(i) >= 'a' && s.charAt(i) <= 'z'){sb.append((char)(s.charAt(i) - 32));dfs(s, i+1, sb);}else if(s.charAt(i) >= 'A' && s.charAt(i) <= 'Z'){sb.append((char)(s.charAt(i) + 32));dfs(s, i+1, sb);}if((s.charAt(i) >= 'a' && s.charAt(i) <= 'z') || (s.charAt(i) >= 'A' && s.charAt(i) <= 'Z'))sb.deleteCharAt(sb.length()-1);}
}

93. 复原 IP 地址

难度中等1146收藏分享切换为英文接收动态反馈

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你不能重新排序或删除 s 中的任何数字。你可以按任何顺序返回答案。

示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

1 <= s.length <= 20
s 仅由数字组成

class Solution {List<String> res = new ArrayList<>(); List<String> tmp = new ArrayList<>();public List<String> restoreIpAddresses(String s) {dfs(s, 0);return res;}public void dfs(String s, int begin){if(tmp.size() == 4 && begin != s.length()) return;if(tmp.size() == 4 && begin == s.length()){res.add(String.join(".",tmp));return;}//枚举分割点for(int j = begin; j < s.length() && j < begin+3; j++){String str = s.substring(begin, j+1);// 每个整数位于 0 到 255 之间组成if(Integer.parseInt(str) <= 255){// 不能含有前导 0if(str.length() > 1 && str.charAt(0) == '0'){return;}tmp.add(str);dfs(s, j+1);tmp.remove(tmp.size()-1);}else{return;}}}
}

组合型回溯（剪枝技巧）

77. 组合

难度中等1284

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> cur = new ArrayList<>();int n, k;public List<List<Integer>> combine(int _n, int _k) {n = _n;k = _k;dfs(1);return res;}public void dfs(int i){if(cur.size() == k){ // d == 0res.add(new ArrayList<>(cur));return;}for(int j = i; j <= n - (k - cur.size()) + 1 ; j++){cur.add(j);dfs(j+1);cur.remove(cur.size() - 1);}}
}

相同方式倒着遍历的写法

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> cur = new ArrayList<>();int n, k;public List<List<Integer>> combine(int _n, int _k) {n = _n; k = _k;dfs(n);return res;}public void dfs(int i){int d = k - cur.size();// 还要选 d 个数if(d == 0){ res.add(new ArrayList<>(cur));return;}for(int j = i; j >= d; j--){cur.add(j);dfs(j-1);cur.remove(cur.size() - 1);}}
}

216. 组合总和 III

难度中等622

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9
每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

2 <= k <= 9
1 <= n <= 60

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> cur = new ArrayList<>();int k;public List<List<Integer>> combinationSum3(int _k, int n) {k = _k;dfs(9, n);return res;}public void dfs(int i, int target){int d = k - cur.size();// 还要选 d 个数//剪枝// 首项+末项 *项数 /2  仍然比target小，就不用递归了if(target < 0 || target > (i*2 - d + 1) * d / 2)return; // d = 0 , (i*2 - d + 1) * d / 2也是等于0的，就不用判断target = 0 了if(d == 0){ res.add(new ArrayList<>(cur));return;}for(int j = i; j >= d; j--){cur.add(j);dfs(j-1, target-j);cur.remove(cur.size() - 1);}}
}

22. 括号生成

难度中等3091

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

1 <= n <= 8

class Solution {int n;char[] path;List<String> res = new ArrayList<>();public List<String> generateParenthesis(int n) {this.n = n;path = new char[n * 2];dfs(0, 0);return res;}public void dfs(int i, int open){if(i == n * 2){res.add(new String(path));}if(open < n){ // 可以填左括号path[i] = '(';dfs(i+1, open+1);}if(i - open < open){ // 不可以填左括号了，只能填右括号}path[i] = ')';dfs(i+1, open);}}
}

排列型回溯（棋盘问题也是排列型回溯）

排列型和组合型的区别：组合中不能有{1，2} {2，1} 同时存在，因为他们是相同的组合

46. 全排列

难度中等2411

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

class Solution {List<List<Integer>> res = new ArrayList<>();List<Integer> cur = new ArrayList<>();boolean[] visit;public List<List<Integer>> permute(int[] nums) {visit = new boolean[nums.length];dfs(0, nums);return res;}public void dfs(int i, int[] nums){if(i == nums.length){res.add(new ArrayList<>(cur));return;}for(int k = 0; k < nums.length; k++){if(visit[k] == false){visit[k] = true;cur.add(nums[k]);dfs(i+1, nums);cur.remove(cur.size()-1);visit[k] = false;}}}}

51. N 皇后

难度困难1648

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

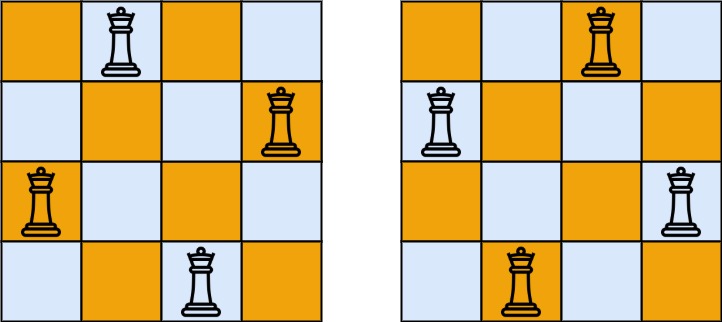
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

1 <= n <= 9

题解：https://leetcode.cn/problems/n-queens/solution/java-c-by-tizzi-i9j0/

class Solution {List<List<String>> ans = new ArrayList<>();int[] row;boolean[] cols, d, ud;int N;public List<List<String>> solveNQueens(int n) {N = n;cols = new boolean[n];d = new boolean[30];ud = new boolean[30];row = new int[n];// 用来保存第几行第几列放置Qdfs(0);return ans;}// col【】数组记录某列已经放过了皇后。col【i】= 1代表第i列已经放了一个皇后。// d【】 数组来记录某正对角线已经放置过了皇后。// ud【】数组来记录某反对角线已经放置过了皇后。public void dfs(int i){if(i == N){char[] arr = new char[N];Arrays.fill(arr, '.');List<String> g = new ArrayList<>();for(int j = 0; j < N; j++){arr[row[j]] = 'Q';g.add(new String(arr));arr[row[j]] = '.';}ans.add(g);return;}// 选择一个位置进行放置for(int j = 0; j < N; j++){// 列，对角线、反对角线判断if (!cols[j] && !d[i + j] && !ud[N - i + j]){cols[j] = d[i+j] = ud[N-i+j] = true;row[i] = j;dfs(i+1);cols[j] = d[i+j] = ud[N-i+j] = false;}}}
}